dynadojo.systems.lds.LDSystem#

class dynadojo.systems.lds.LDSystem#

Bases: SimpleSystem

Linear dynamical system (LDS). Implements an LDS of the form \(\dot{x} = Ax + Bu\) where \(Ax\) is the drift term of \(\dot{x}\) and \(Bu\) is input term of \(\dot{x}\).

Example

>>> from dynadojo.systems.lds import LDSystem
>>> from dynadojo.wrappers import SystemChecker
>>> from dynadojo.utils.lds import plot
>>> latent_dim = 9
>>> embed_dim = 14
>>> n = 500
>>> timesteps = 50
>>> system = SystemChecker(LDSystem(latent_dim, embed_dim, noise_scale=0, seed=0))
>>> x0 = system.make_init_conds(n)
>>> y0 = system.make_init_conds(30, in_dist=False)
>>> x = system.make_data(x0, timesteps=timesteps)
>>> y = system.make_data(y0, timesteps=timesteps, noisy=True)
>>> plot([x, y], target_dim=min(latent_dim, 3), labels=["in", "out"], max_lines=15)

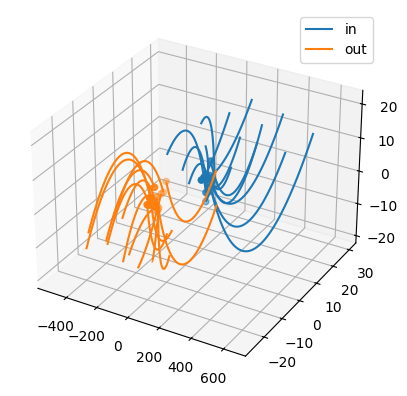
>>> from dynadojo.baselines.dmd import DMD
>>> from dynadojo.challenges import FixedTrainSize
>>> challenge = FixedTrainSize(L=[2, 3, 4, 5], E=None, t=50, n=10, reps=10, system_cls=LDSystem, test_examples=1, test_timesteps=50, max_control_cost_per_dim=0, control_horizons=0)
>>> data = challenge.evaluate(algo_cls=DMD)
>>> challenge.plot(data)

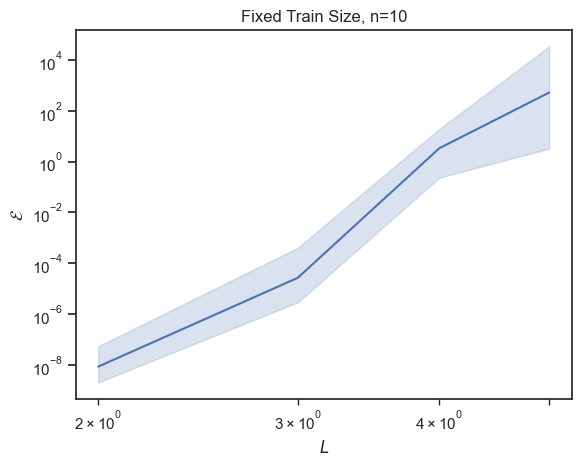
Methods

`__init__`([latent_dim, embed_dim, ...])	Initialize the class.
`calc_control_cost`(control)	Calculates the L2 norm / dimension of every vector in the control
`calc_dynamics`(t, x)	Calculates the dynamics for the system.
`calc_error`(x, y)	Returns the MSE error normalized by the embedded dimension.
`make_data`(init_conds, control, timesteps[, ...])	Uses the `calc_dynamics()` method to generate data.
`make_init_conds`(n[, in_dist])	Uniformly samples embedded-dimensional points from an inside or outside distribution

Attributes

`controller`	The controller matrix.
`embed_dim`	The embedded dimension for the system.
`embedder`	The embedder matrix.
`latent_dim`	The latent dimension for the system.
`seed`	The random seed for the system.

__init__(latent_dim=2, embed_dim=2, A_eigval_range=(-1, 1), A_eigvec_range=(-1, 1), **kwargs)#

Initialize the class.

Parameters:

latent_dim (int, optional) – Dimension of the latent space. Defaults to 2. Can set to large values.
embed_dim (int, optional) – Embedded dimension of the system. Defaults to 2. Can set to large values. Should be at least as large as latent_dim.
A_eigval_range (tuple, optional) – Range for eigenvalues of the matrix A. Defaults to (-1, 1). Recommended to keep this value between -1 and 1 for stable systems.
A_eigvec_range (tuple, optional) – Range for eigenvectors of the matrix A. Defaults to (-1, 1).
**kwargs – Additional keyword arguments.

calc_control_cost(control)#

Calculates the L2 norm / dimension of every vector in the control

Parameters:: control (ndarray) –
Return type:: float

calc_dynamics(t, x)#: Calculates the dynamics for the system. Your class must implement this.

calc_error(x, y)#

Returns the MSE error normalized by the embedded dimension.

Return type:: float

property controller#: The controller matrix. For example, in a system \(\dot{x} = Ax + Bu\), the controller is \(B\).

property embed_dim#: The embedded dimension for the system.

property embedder#: The embedder matrix. An invertible map from the latent space to the embedding space.

property latent_dim#: The latent dimension for the system.

make_data(init_conds, control, timesteps, noisy=False)#

Uses the calc_dynamics() method to generate data. Mathematically, data is generated like \(\dot{x} = f(x) + Bu\). Where \(f(x)\) is given by calc_dynamics().

Parameters:

init_conds (numpy.ndarray) – (n, embed_dim) Initial conditions matrix.
control (numpy.ndarray) – (n, timesteps, embed_dim) Controls tensor.
timesteps (int) – Timesteps per training trajectory (per action horizon).
noisy (bool, optional) – If True, add noise to trajectories. Defaults to False. If False, no noise is added.

Returns:

(n, timesteps, embed_dim) Trajectories tensor.

Return type:

numpy.ndarray

make_init_conds(n, in_dist=True)#

Uniformly samples embedded-dimensional points from an inside or outside distribution

Note

Systems developers determine what counts as in vs out-of-distribution. DynaDojo doesn’t provide any verification that this distinction makes sense or even exists. See LDSystem for a principled example.

Parameters:

n (int) – Number of initial conditions.
in_dist (bool, optional) – If True, generate in-distribution initial conditions. Defaults to True. If False, generate out-of-distribution initial conditions.

Returns:

(n, embed_dim) Initial conditions matrix.

Return type:

numpy.ndarray

property seed#: The random seed for the system.