dynadojo.baselines.dmd.DMD#

class dynadojo.baselines.dmd.DMD#

Bases: AbstractAlgorithm

Dynamic mode decomposition. Implementation uses the pydmd library [1].

Note

For an example of DMD with a challenge, see LDSystem.

References

Example

from dynadojo.systems.lds import LDSystem
from dynadojo.wrappers import SystemChecker
from dynadojo.utils.lds import plot

latent_dim = 3
embed_dim = 10
n = 15
timesteps = 20
system = SystemChecker(LDSystem(latent_dim, embed_dim, noise_scale=0, seed=2))
x0 = system.make_init_conds(n)
y0 = system.make_init_conds(30, in_dist=False)
x = system.make_data(x0, timesteps=timesteps)
y = system.make_data(y0, timesteps=timesteps, noisy=True)
plot([x, y], target_dim=min(latent_dim, 3), labels=["in", "out"], max_lines=15)
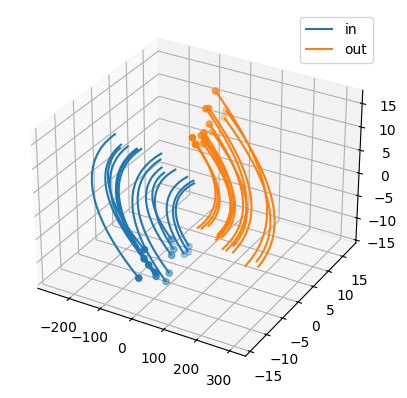
../_images/dmd1.png 
from dynadojo.baselines.dmd import DMD
from dynadojo.wrappers import AlgorithmChecker

dmd = AlgorithmChecker(DMD(embed_dim, timesteps, activation=None, max_control_cost=0))
dmd.fit(x)
x_pred = dmd.predict(x[:, 0], timesteps)
y_pred = dmd.predict(y[:, 0], timesteps)
plot([x_pred, y_pred], target_dim=min(3, latent_dim), labels=["in pred", "out pred"], max_lines=15)
x_err = system.calc_error(x, x_pred)
y_err = system.calc_error(y, y_pred)
print(f"{x_err=}")
print(f"{y_err=}")

Both errors should be around 0 and the predictions looks like this:

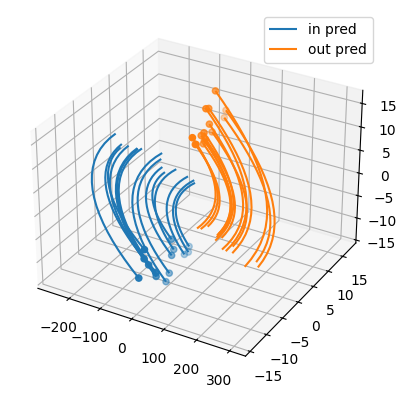
../_images/dmd2.png

Methods

__init__(embed_dim, timesteps[, ...])

Initialize the class.

act(x, **kwargs)

Determines the control for each action horizon.

fit(x, **kwargs)

Fits the algorithm on a tensor of trajectories.

predict(x0, timesteps, **kwargs)

Predict how initial conditions matrix evolves over a given number of timesteps.

Attributes

embed_dim

The embedded dimension of the dynamics.

max_control_cost

The maximum control cost.

seed

The random seed for the algorithm.

timesteps

The timesteps per training trajectory.
__init__(embed_dim, timesteps, max_control_cost=0, **kwargs)#

Initialize the class.

Parameters:

  • embed_dim (int) – Recommended embedding dimension should be <5.

  • timesteps (int) – Timesteps in the training trajectories.

  • max_control_cost (float) – Ignores control, defaults to 0.

  • **kwargs – Additional keyword arguments.

act(x, **kwargs)#

Determines the control for each action horizon. control.

Parameters:

  • x (numpy.ndarray) – (n, timesteps, embed_dim) Trajectories tensor.

  • **kwargs – Additional keyword arguments.

Returns:

(n, timesteps, embed_dim) controls tensor.

Return type:

numpy.ndarray

property embed_dim#

The embedded dimension of the dynamics.

fit(x, **kwargs)#

Fits the algorithm on a tensor of trajectories.

Parameters:

  • x (np.ndarray) – (n, timesteps, embed_dim) Trajectories tensor.

  • **kwargs – Additional keyword arguments.

Return type:

None

property max_control_cost#

The maximum control cost.

predict(x0, timesteps, **kwargs)#

Predict how initial conditions matrix evolves over a given number of timesteps.

Note

The timesteps argument can differ from the ._timesteps attribute. This allows algorithms to train on a dataset of a given size and then predict trajectories of arbitrary lengths.

Note

The first coordinate of each trajectory should match the initial condition x0.

Parameters:

  • x0 (np.ndarray) – (n, embed_dim) initial conditions matrix

  • timesteps (int) – timesteps per predicted trajectory

  • **kwargs – Additional keyword arguments.

Returns:

(n, timesteps, embed_dim) trajectories tensor

Return type:

np.ndarray

property seed#

The random seed for the algorithm.

property timesteps#

The timesteps per training trajectory.