dynadojo.systems.ca.CASystem#

class dynadojo.systems.ca.CASystem#

Bases: AbstractSystem

Cellular automaton (CA). Implements a one-dimensional CA.

Example

>>> from dynadojo.utils.ca import plot
>>> from dynadojo.wrappers import SystemChecker
>>> latent_dim = 3
>>> embed_dim = 64
>>> timesteps = 30
>>> n = 10
>>> system = SystemChecker((latent_dim, embed_dim, seed=1))
>>> x0 = system.make_init_conds(n=n)
>>> x = system.make_data(x0, timesteps=timesteps)
>>> plot([x], labels=["X"])

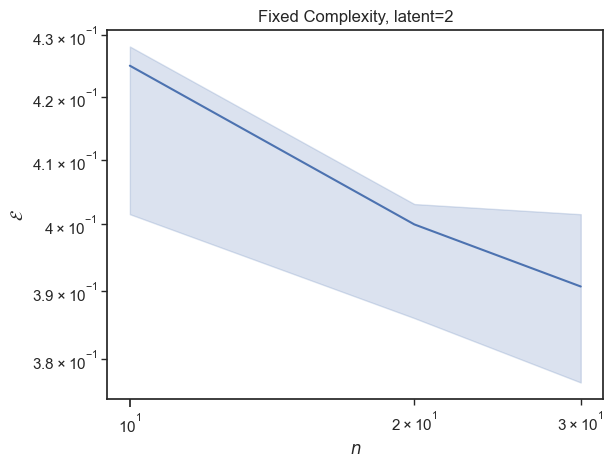
>>> from dynadojo.challenges import FixedComplexity
>>> from dynadojo.baselines.cnn import CNN
>>> challenge = FixedComplexity(l=2, e=64, t=10, N=[10, 20, 30], reps=3, system_cls=CASystem, test_examples=1, test_timesteps=5)
>>> data = challenge.evaluate(algo_cls=CNN)
>>> challenge.plot(data)

Methods

`__init__`([latent_dim, embed_dim, in_dist_p, ...])	Initializes a CASystem instance.
`calc_control_cost`(control)	Calculate the control cost for each control trajectory (i.e., calculates the costs for every control matrix, not for the whole tensor).
`calc_error`(x, y)	Calculates the error between two tensors of trajectories.
`make_data`(init_conds, control, timesteps[, ...])	Makes trajectories from initial conditions.
`make_init_conds`(n[, in_dist])	Generate initial conditions..

Attributes

`embed_dim`	The embedded dimension for the system.
`latent_dim`	The latent dimension for the system.
`seed`	The random seed for the system.

__init__(latent_dim=2, embed_dim=64, in_dist_p=0.25, out_dist_p=0.75, mutation_p=0.0, seed=None)#

Initializes a CASystem instance.

Parameters:

latent_dim (int) – The radius of the CA.
embed_dim (int) – The number of cells in each row of the grid.
in_dist_p (float) – The parameter of the binomial that generate the initial condition for in distribution initial conditions.
out_dist_p (float) – The parameter of the binomial that generate the initial condition for out-of-distribution initial conditions.
mutation_p (float) – If noisy, mutation_p is the chance that any cell of completed generation is flipped. For example, with mutation_p = 1, an unmutated generation 0010 would become 1101.

calc_control_cost(control)#

Calculate the control cost for each control trajectory (i.e., calculates the costs for every control matrix, not for the whole tensor).

Parameters:: control (numpy.ndarray) – (n, timesteps, embed_dim) Controls tensor.
Returns:: (n,) Control costs vector.
Return type:: numpy.ndarray

calc_error(x, y)#

Calculates the error between two tensors of trajectories.

Parameters:

x (numpy.ndarray) – (n, timesteps, embed_dim) Trajectories tensor.
y (numpy.ndarray) – (n, timesteps, embed_dim) Trajectories tensor.

Returns:

The error between x and y.

Return type:

float

property embed_dim#: The embedded dimension for the system.

property latent_dim#: The latent dimension for the system.

make_data(init_conds, control, timesteps, noisy=False)#

Makes trajectories from initial conditions.

Parameters:

init_conds (numpy.ndarray) – (n, embed_dim) Initial conditions matrix.
control (numpy.ndarray) – (n, timesteps, embed_dim) Controls tensor.
timesteps (int) – Timesteps per training trajectory (per action horizon).
noisy (bool, optional) – If True, add noise to trajectories. Defaults to False. If False, no noise is added.

Returns:

(n, timesteps, embed_dim) Trajectories tensor.

Return type:

numpy.ndarray

make_init_conds(n, in_dist=True)#

Generate initial conditions..

Note

Systems developers determine what counts as in vs out-of-distribution. DynaDojo doesn’t provide any verification that this distinction makes sense or even exists. See LDSystem for a principled example.

Parameters:

n (int) – Number of initial conditions.
in_dist (bool, optional) – If True, generate in-distribution initial conditions. Defaults to True. If False, generate out-of-distribution initial conditions.

Returns:

(n, embed_dim) Initial conditions matrix.

Return type:

numpy.ndarray

property seed#: The random seed for the system.